Digital Logic Circuits and Components

• Digital Computers
• Logic Gates, Boolean Algebra
• Map Simplifications
• Combinational Circuits
• Flip-Flops
• Sequential Circuits
• Integrated Circuits
• Decoders
• Multiplexers
• Registers and Counters
• Memory Unit.

Digital Computers

A digital computer is an electronic machine that processes information using binary (0s and 1s). It consists of:

• Central Processing Unit (CPU): Controls operations and executes instructions.
• Memory (RAM, ROM): Stores data and programs.
• Input/Output (I/O) Devices: Communicates with external devices.
• Bus System: Transfers data between components.

A digital computer works on binary arithmetic and logic operations, making digital logic circuits fundamental to its operation.

---

Logic Gates

Logic gates are the basic building blocks of digital circuits. They process binary signals (0 and 1) based on Boolean algebra.

Basic Gates:

Gate	Symbol	Operation
AND	∧	Output is 1 if both inputs are 1
OR	∨	Output is 1 if at least one input is 1
NOT	¬	Inverts the input (0 → 1, 1 → 0)

Universal Gates:

• NAND (NOT AND): Output is 0 only if both inputs are 1.
• NOR (NOT OR): Output is 1 only if both inputs are 0.
• XOR (Exclusive OR): Output is 1 if inputs are different.
• XNOR (Exclusive NOR): Output is 1 if inputs are the same.

NAND and NOR gates are universal because all logic circuits can be built using only them.

---

3. Boolean Algebra

Boolean algebra simplifies digital circuits using logical operations:

• Idempotent Law: A + A = A, A · A = A
• Complement Law: A + A’ = 1, A · A’ = 0
• De Morgan’s Theorem:
  • (A · B)’ = A’ + B’
  • (A + B)’ = A’ · B’

Boolean algebra helps in simplifying logic circuits by reducing the number of gates.

Absolutely! Let’s stick with the “light switch” + kid-friendly style to explain these three important concepts in Boolean Algebra.

---

Idempotent Law:

“Doing it twice is the same as doing it once.”

1. A + A = A

Imagine you have a switch A.
If you say “If A is ON OR A is ON”, that’s still just A is ON.

🧠 You’re not making it any more ON by repeating it.

A	A + A
0	0
1	1

2. A · A = A

This is like saying “A AND A” — which is still just A.

🧠 If the same switch is needed twice to turn on the light, it’s no different from needing it once.

A	A · A
0	0
1	1

---

Complement Law:

“A and its opposite always cancel out.”

1. A + A' = 1

This is like saying:

💡 “If switch A is ON OR switch A is OFF, will the light turn ON?”
Yes! One of them has to be true.

A	A’	A + A’
0	1	1
1	0	1

2. A · A' = 0

💡 “If switch A is ON AND A is OFF at the same time?”
That can never happen — it’s a contradiction. So the light is OFF.

A	A’	A · A’
0	1	0
1	0	0

---

De Morgan’s Theorem:

“Flip the group, change AND to OR (or OR to AND).”

This is a magic trick to simplify logic when there’s a NOT outside a group.

1. (A · B)' = A' + B'

Say:
“If both A AND B need to be ON for light, and I say NO to that, what’s actually happening?”
👉 You’re saying: “Either A is OFF OR B is OFF”

A	B	A·B	(A·B)‘	A’	B’	A’+B’
0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	0	1	1
1	1	1	0	0	0	0

✅ Left and right sides match!

---

2. (A + B)' = A' · B'

“If A OR B turns the light ON, and I say NO to that, it means BOTH A and B must be OFF.”

A	B	A+B	(A+B)‘	A’	B’	A’·B’
0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

✅ Both sides match again!

---

4. Map Simplifications (Karnaugh Map - K-Map)

A K-map is a visual method of simplifying Boolean expressions by grouping adjacent 1s in a truth table.

• Uses 2, 3, 4, or more variables.
• Groups 1s in powers of 2 (1, 2, 4, 8).
• Reduces complex logic functions into minimal SOP (Sum of Products) or POS (Product of Sums) form.

Example:

  AB | 00 | 01 | 11 | 10 |
 --- |----|----|----|----|
   0 |  0 |  1 |  1 |  0 |
   1 |  1 |  1 |  0 |  0 |

Groups: (A’B) + (AB’)

Result: A ⊕ B (XOR Gate)

---

5. Combinational Circuits

Combinational circuits do not store past inputs (no memory). Their output depends only on the current inputs.

Examples:

1. Half Adder – Adds two binary digits (A, B)
   • Sum (S) = A ⊕ B
   • Carry (C) = A · B

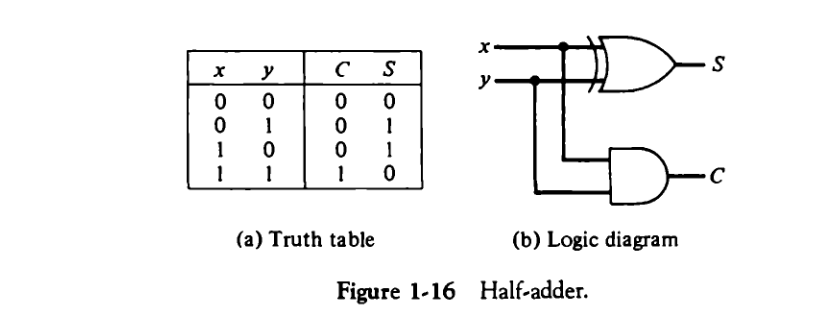
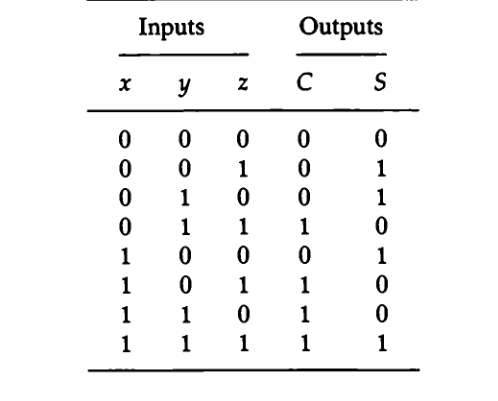
1. Full Adder – Adds three binary digits (A, B, Carry-in)
   • Sum (S) = A ⊕ B ⊕ Cin
   • Carry (Cout) = A · B + Cin (A ⊕ B)

1. Subtractor: Performs binary subtraction using XOR, AND, and NOT gates.

2. Multiplexer (MUX): Selects one input from multiple inputs based on a selector.

   • 2:1 MUX: Y = S’ A + S B

3. Demultiplexer (DEMUX): Sends one input to multiple outputs.

---

6. Flip-Flops (Sequential Circuits)

Flip-flops are memory elements that store one bit. They are the building blocks of registers and counters.

Types of Flip-Flops:

Type	Symbol	Function
SR Flip-Flop	S-R	Stores data based on Set (S) and Reset (R) inputs
D Flip-Flop	D	Stores input D at clock pulse
JK Flip-Flop	J-K	Eliminates indeterminate state of SR flip-flop
T Flip-Flop	T	Toggles between 0 and 1

Example: D Flip-Flop Truth Table

D	Q(next)
0	0
1	1

Clocked Flip-Flops are used in counters, registers, and memory units.

---

7. Integrated Circuits (ICs)

Integrated Circuits combine multiple logic gates on a chip.

IC Classifications:

1. SSI (Small Scale Integration) – Few gates (AND, OR, XOR)
2. MSI (Medium Scale Integration) – Adders, Decoders, Multiplexers
3. LSI (Large Scale Integration) – Processors, Memory Chips
4. VLSI (Very Large Scale Integration) – Microprocessors, FPGAs

VLSI circuits power modern CPUs, GPUs, and embedded systems.

---

8. Decoders

A decoder converts binary inputs into a single active output.
Example: 2-to-4 Decoder

A	B	Output
0	0	0001
0	1	0010
1	0	0100
1	1	1000

• Used in memory address decoding.

---

9. Multiplexers

A multiplexer (MUX) selects one input from many based on control lines.

Example: 4-to-1 MUX
Y = A S0’ S1’ + B S0 S1’ + C S0’ S1 + D S0 S1

• Used in data routing and CPU registers.

---

10. Registers and Counters

A register is a group of flip-flops used for temporary storage of data in CPUs.

• Shift Registers: Shift data left or right (used in serial communication).
• Parallel Registers: Store multiple bits at once.

A counter is a register that increments or decrements values based on clock pulses.

Types of Counters:

1. Asynchronous Counter – Ripple effect (slower)
2. Synchronous Counter – All flip-flops triggered at the same time (faster)
3. Up/Down Counter – Counts up or down based on control input
4. Ring Counter – Circular shift of bits

---

11. Memory Unit

A memory unit stores and retrieves data in a digital system.

Types of Memory:

1. Primary Memory (RAM, ROM) – Fast, volatile (RAM), non-volatile (ROM)
2. Cache Memory – Small, fast memory between CPU and RAM
3. Secondary Memory (HDD, SSD) – Stores permanent data
4. Registers – High-speed temporary storage in CPU

Memory is organized as word addressable or byte addressable.

---